Humdrum Extras

tntype manpage

COMMAND

    tntype -- Extract set-theory Tn types from **kern sonorities in Humdrum files.

SYNOPSIS

    tntype [-adDfiInpPrStvx] [input] [> output]

OPTIONS

ⓘ-a Append extracted information to original input data.
ⓘ-d Display the diatonic pitch classes of notes in the sonority.
ⓘ-D Display a musical description of the Tn type for the isolated pitch-classes present in the sonority.
ⓘ-f Display Tn form rather than type.
ⓘ-F Display Forte-style prime-form types rather than Tn types.
ⓘ-i Display the interval vector of the sonority.
ⓘ-k Inculde all pitch-class subsets when analyzing Tn names.
ⓘ-I Do not display the inversion variant of the Tn type (usually equivalent to prime-form's type).
ⓘ-n Display sonority pitch-class sets in normal form.
ⓘ-p Display sonority pitch-class sets in prime form.
ⓘ-r Indicate which pitch in the sonority is lowest.
ⓘ-S Do not display parentheses around diatonic pitch classes that are only sustained from previous sonorities.
ⓘ-t Indicate transposition relation between normal and Tn forms.
ⓘ-v Give verbose Tn types with extra information about they type.
ⓘ-x Mark sonorities with an "x" if all pitches in the sonority start within sonority, or with an "s" if one or more notes are sustained from a previous sonority,

DESCRIPTION
    The tntype program extracts Tn categories of pitch-class sets delineated by sonorities in Humdrum **kern data. Tn types are the normal form of a pitch-class set with the first element transposed to 0. Unlike the prime form (which is a 'Tn/TnI' type), Tn types can distinguish between pitch-class sets that represent major and minor triads. This makes Tn types more suitable for harmony analysis in tonal music than Tn/TnI types.

    The following figure shows how the Tn type is calculated from the normal form of a pitch-class set by shifting the first pitch class of the normal form to 0. For G major, the pitch-classes (relative to C=0) are G=7, B=11, and D=2 when placed in normal form. Then, subtract 7 from each number (modulo 12) to get the form which describes the Tn type: 0, 4, 7. Notice that the two chords in the figure are mirror images of each other since the intervals up from the D pitch for the minor chord are the same intervals going down in the major chord (also called an inversion in set theory).

    Since major and minor chords are inversions (in the set-theory sense) of each other, they have the same prime form which is 037, because the Tn type for a minor-chord pitch-class set is a more compact description of the intervals. Note that the Tn/TnI type (prime form) searches all possible transpositions and inversions of an normal-formed pitch-class set to find the most compact intervallic description of the pitch-class set, while the Tn type only searches all possible transpositions for the most compact form.

    Tn/TnI types can be described uniquely either by the prime form or by the Forte number of the prime form. The Forte number is two integers separated by a dash, with the first number being a count of the pitch-classes in the set (the cardinality), and the second number being an enumeration of all prime forms for that cardinality sorted by compactness. For example, major and minor triad pitch-class sets have a cardinality of 3, and the prime form 037 is the 11th most compact form for cardinality 3; therefore, the Forte number for these two chord types is 3-11.

    The Tn types can also be summarized using Forte numbers. To do so, use the same Forte number as the Tn/TnI type (prime form). Then, follow the Forte number by an "A" if the Tn type has the same form as the prime from, or a "B" if the Tn type is an inversion of the prime form. However, if the prime form and the inversion of the prime form are equal, the "A"/"B" variant labels are not appended to the Forte number (since they are equivalent).

    An example of a non-invertible pitch class set is (C, F and G). The prime form of this pitch-class set is (0, 2, 7). If the prime form is inverted: (12-0, 12-2, 12-7) = (0, 10, 5) → (0, 5, 10) → (10, 0, 5) → (0, 2, 7) which is the same form as the initial prime form. In this case the Tn type expressed as a Forte number is 3-9, with no "A" or "B" alteration since the prime form inverts to itself.

    Since a minor triad's pitch classes generate their prime form without the need for an inversion, a minor chord expressed as a Tn type using Forte numbers is 3-11A. In this case, the "A" indicates that the prime form (Tn/TnI type) does not need to be inverted to express the Tn type. The pitch-classes of a major chord do need to be inverted to arrive at their prime form; therefore, the Tn type for a major chord is 3-11B. In this case, the "B" indicates that the prime form needs to be inverted to generate the (transposed) normal form.

    The following figure summarizes the various set-theory descriptions of pitch-class sets, starting with the prime form which is the most reduced description of a set, then progressing to more explicit descriptions of the pitch classes, using major and minor triads as the example pitch-class sets. Note that the prime form (Tn/TnI type) bifurcates into two Tn types which are the regular and inverted forms of the prime form (unless the prime form is inversionally symmetric). In turn, a Tn type splits into twelve normal forms, although rotational symmetry will reduce certain normal forms to submultiples of 12 (1, 2, 3, 4, 6). The normal form, in turn, can be expressed in theory as an infinite number of diatonic spellings, although in practice only one or two diatonic variants will be common in actual musical notation. For example, the normal form (4, 7, 10, 0) can represent (C, E, G, B♭) which is a dominant seventh chord, or (C, E, G, A♯) which is a German augmented-sixth chord. In this case, A♯ hints that the next note to follow will be a B♮, while B♭ hints that the next note to follow will be A♮. As an aside, for 12-tone pitch-class sets, there are 216 prime forms (Tn/TnI types) which includes the null pitch-class set representing a rest, 351 Tn types which adds 128 inversional variants, and 4096 possible normal forms (212).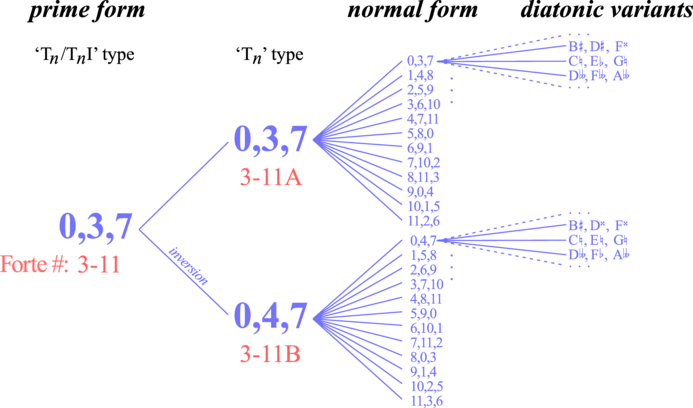

    By default, the tntype program reports The Tn type using Forte numbers. Using the -a option will append the extracted Tn types at the end of each line of the original input data, as illustrated on the right in the examples below. 

    tntype input
    		 
    tntype -a input

    The -k option will display all subsets for an input form: 

    tntype -ak input

    The Tn type's form, rather than Forte number, can be extracted by using the -f option. The example program call on the right below shows how to display both the Forte number and form of the Tn type at the same time by passing the input data through the tntype program twice. 

    tntype -fa input
    		 
    tntype -a input | tntype -fa

    The -D option can be used to give a musically oriented description of the pitch-class sets, which is useful for interpreting the musical implication of the Tn type: 

    tntype -a input | tntype -fa | tntype -Da > output

    **kern**tnt**tnf**description
    g b d3-11B{047}Major Chord
    d f a3-11A{037}Minor Chord
    c f g3-9{027}Quartal Trichord
    g b d f4-27B{0368}Dominant-seventh/German-sixth Chord
    g b d e#4-27B{0368}Dominant-seventh/German-sixth Chord
    c e- g- b--4-28{0369}Diminished-seventh Chord
    f b d# g#4-27A{0258}Half-diminished Seventh Chord/Tristan Chord
    c f# b- e a d6-34A{013579}Mystic Chord or Prometheus Hexachord/comb I (B)
    *-*-*-*-

    Sonorities

    Humdrum encodings of musical scores give a timewise sequence of events in the music. Each line in the data represents the notes which are currently sounding at that time. If a new note is starting on a line, then a note will be given; otherwise, a sustained note from a previous line will be represented by a dot in its spine (column). Therefore, each data line in the Humdrum score represents a vertical sonority of pitches which can be reduced to pitch-class set.

    In the following illustration, the first data line in the Humdrum data represents a sonority with the pitches "A, c, a, cc". The second data line has one new pitch (G3) as well as three notes held over from the previous line/sonority: c, a, and cc.

    This example contains seven sequential static sonorities which are numbered in the following figure. Some of the sonorities (1, 3, 5, 7) contain only notes which are started at the beginning of the segmentation boundaries for the sonority, while others (2, 4, and 6) contain notes started in previous sonorities and sustained into the current sonority, which are highlighted in red.

    The -d option will give a list of the diatonic pitch classes present in each sonority, with the lowest note capitalized and pitch classes which are only sustained from previous sonorities in parentheses. This initial reduction of the pitches in the sonority is used as a basis for further reductions and analysis of the sonorities within the tntype program. In an analogue to intervallic compactness used to sort notes in normal and prime forms in set theory, the diatonic pitch classes are arranged in the triadically most compact form. Thus, if the sonority represents a triadic chord built up from thirds, the first element will represent the root of the chord. If there are non-harmonic tones present in the sonority, this will not necessarily be true. 

    tntype -da input > output

    Normal form

    The twelve-tone analogue of the -d option is the -n option which sorts the pitch-class set of the sonority into normal form which is the most compact interval representation of the pitch classes. The normal form for displaying the pitch-class set orders the notes chromatically, and selects the rotation of the sorted set that minimizes the intervals created between the first pitch class in the list, prioritized from the end of the list. For example, the pitch class ordering (A, C, E) is more compact than the ordering (C, E, A), since the first ordering has an interval of a perfect fifth between the first and last pitch class, whereas the second ordering has a major sixth. If more than one rotation has the same outer interval, the next smallest interval is used as a tie-breaker, and so on. Some pitch-class sets have rotation symmetries, such as (A, C, E♭, G♭), which is equally compact in any base-12 rotation. 

    tntype -na input > output

    The normal form of the pitch-class set is enclosed in square brackets to distinguish it from other pitch-set forms, with each digit representing a particular pitch-class, with 0=C, 2=D, 4=E, 5=F, etc. The last two pitch classes are represented in tntype output by the base-12 numerical digits A and B so that each pitch-class is represented by a single digit:

    decimal
    name    		base-12 diatonic
    name
    00 B♯, C♮
    11 C♯, D♭
    22 D♮
    33 D♯, E♭
    44 E♮, F♭
    55 E♯, F♮
    decimal
    name    		base-12 diatonic
    name
    66 F♯, G♭
    77 G♮
    88 G♯, A♭
    99 A♮
    10A A♯, B♭
    11B B♮, C♭

    Tn type (form-based description)

    The normal form gives an explicit list of pitch-classes, but cannot directly be used to identify transpositions of the same intervallic configurations starting on different pitch classes. For example, (G, B♭, D) and (C, E♭, G) are both minor chords. The similarity between these two sets is only observable at the Tn level of pitch-class reduction, since they are different at the normal-form level. The two chords' normal forms are [7A2] and [037], and the fact that they are both minor chords are hidden because they have different roots. Therefore, the pitch-class sets can be represented in the Tn form to reveal this similarity between them by tranposing them so that their first elements are set to the same value (to 0 by convention). Calculating the Tn form from the normal form is easy: subtract the first pitch-class value in the normal form from all pitch-classes in the normal form. For G minor, represented by [7A2], subtract 7 from each pitch class: 7-7=0, 10-7=3, 2-7=14-7=7 → {037}.

    To extract the Tn form from the **kern data in input Humdrum data, use the -f option: 

    tntype -af input > output

    To distinguish between the normal form and the Tn type's form in tntype data output, the Tn type's form is enclosed in curly braces. Note that the Tn type's form is just the normal form of a pitch-class set with the first pitch class being 0. To preserve the transposition value needed to convert from the normal form to the Tn type's form, use the -t option to append the transposition amount that can be added to the Tn type's form to recover the normal form of the pitch-class set. 

    tntype -an input | tntype -aft > output

    Tn type (as Forte numbers)

    Besides describing the Tn type as a 0-transposed normal form, the Tn type can be given an arbitrary name which is analogous to labelling (G, B♭, D) as a minor chord. The standard method of naming pitch-class sets is to specify the number of (unique) pitch-classes in the set, which is formally called the cardinality of a set in set theory, followed by a dash and then an enumeration integer calculated by ordering all prime-forms for that cardinality by intervallic compactness. This is called the Forte number of a pitch-class set.

    Prime forms of pitch-class sets are the result of applying transposition and inversion operations to the normal form in order to (almost) uniquely describe the interval composition of the set in terms of pitch classes. Note that in set theory, inversion means that the intervals between pitch-classes are negated (such as 7 steps up for a perfect fifth becomes 7 steps down), while in tonal music theory, inversion is a rotation of a chord's pitch classes as sorted starting at the root and going up by thirds.

    Note in particular that the inversion operation used to calculate a prime form may change the pitch-class composition of a set, while the intervals between the picth-classes will remain constant. For example, major and minor chords are set-theory inversions of each other, with both containing the same intervals generated from permutations of their pitch class sets: a minor third, a major third, and a perfect fifth. However, major and minor chords cannot be represented by the same normal forms, since one pitch-class will always be different, such as (C, E, G) for C major and (C, E♭, G) for C minor.

    Essentially, C major and C minor sonorities have a very different sound because each pitch is physically composed of harmonics, and these harmonics cannot be set-theory inversed (except perhaps in computer-generated sounds). Therefore, reducing pitch-class sets to their prime forms will merge perceptually relevant differences between inversionally related pitch classes. Thus it is useful for harmony-analysis purposes to not reduce normal forms all of the way to prime forms, but rather describe them as a Tn type which will not inversionally collapse two intervallically identical pitch-class sets consisting of different pitch classes into a single prime form. By using the "A" and "B" alternate versions of the Forte-number names for the prime formes, These inversionally related Tn types can both preserve their intervallic equivalence at the same time as remaining distinct.

    Here is a summary of the relation between various descriptions of a major and minor chord going from a musical sonority through reductions into the prime form:

    D major
    G minor
    diatonic pitches A3, F♯4, A4, D5 B♭3, D4, G4, D5
    base-12 pitches 57, 66, 69, 74 58, 62, 67, 74
    diatonic pitch classes A, D, F♯, D B♭, D, G, D
    base-12 pitch classes 9, 2, 6, 2 10, 2, 7, 2
    diatonic pitch-class set A, D, F♯ B♭, D, G
    base-12 pitch-class set 9, 2, 6 10, 2, 7
    diatonic normal type D, F♯, A G, B♭, D
    base-12 normal type 2, 6, 9 7, 10, 2
    diatonic Tn type (as a form) P1, M3, P5 P1, m3, P5
    base-12 Tn type (as a form) 0, 4, 7 0, 3, 7
    musical chord name major minor
    Tn type (as a Forte #) 3-11B 3-11A
    diatonic prime form m3, M3, P5 m3, M3, P5
    base-12 prime form 0, 3, 7 0, 3, 7
    prime type 3-11 3-11
    base-12 interval vector 001110 001110

    Other options

    Musical description of Tn types

    The -D option will produce an output spine with textual descriptions of the pitch-class set found in the sonority occurring on each line. 

    tntype -Da input > output

    Tn/TnI type (as the prime form)

    Prime-form output may be added in the future. The prime form of a pitch-class set is the most intervally compact chromatic arrangement of pitch-classes in a set when considering both transpositions and inversions of the normal form. See the Humdrum toolkit program pcset which can calculate prime forms: 

    semits -x input | ditto | pcset -p > output1
    semits -x input | ditto | pcset > output2   
    output 1
    output 2

    Using the standard Humdrum Toolkit program pcset, note that you first convert **kern data into absolute base-12 pitches (with middle C being 0, B3=-1 and D4=2) by using the semits Humdrum tool. The -x option is used to remove rhythmic values from the kern data, so that they do not turn the **semits data into junk. Next, the data is sent through the Humdrum tool called ditto which is used to convert null-tokens into the token which they represent; otherwise, pcset will ignore pitches continued from previous lines by the null-tokens.

    Tn/TnI types (Prime-form Forte numbers)

    Use the -P option to display the prime form's type which is the same as the Tn type but without the A/B variants.

    Don't mark inversion variants

    Identical results (hopefully) as the -P option, but generated directly from the Tn type rather than from the prime form. When the -I option is used, the inversional variant letters A/B will not be displayed.

    Lowest-note rotation in Tn-type/normal forms

    The -r option will add a marker indicating the rotation of the Tn form that represents the lowest pitch present in the sonority. A lower-case "a" indicates that the lowest note in the sonority is the first note in the Tn type's form (or the normal form), "b" indicates the lowest note is the second pitch class in the Tn form, etc. The -r option can be used alone to append the rotation value to the end of the Tn type's Forte-number label, as well as with the -f option which is used to generate the Tn form and with the -n option which is used to generate the normal form of the sonority's pitch-class set. Note that a rotational marker for prime forms does not make sense if an inversion operation was used to create the prime form from the normal form. 
    tntype -ra measure2.krn  | tntype -far | tntype -nar

    The bass rotation value for 3-11 types is equivalent to tonal-theory chord inversions for major and minor triads:

    For seventh chords, the rotation value for the lowest note in the sonority does not map directly to a chordal inversion. For example, in a dominant seventh chord, the Tn form places the third in the first location of the form:

    For chords with rotational symmetry, the rotation value reported by the -r option will have an ambiguous meaning. For example, a fully diminished seventh chord, such as (A, C, E♭, G♭) is represented in Tn form as {0 3 6 9}, with "0" able to represent any of the pitch classes in the normal form. See the -v option which can mark Tn type symmetries, such as 4-28S3 for the fully diminished seventh chord which has a Tn type of "4-28" and a rotational symmetry of 3. If the verbose label contains the letter "S", then the rotation marker is irrelevant since there are multiple possibilities.

    Interval vector

    An interval vector describes the intervals generated between pitch-classes in a pitch class set. It is a list of 6 numbers which enumerate counts of intervals from 1 to 6 semitone between the permutations of the pitch-classes in the set. For example (C, E, G) has an interval vector of <001110> since it has 0 minor seconds, 0 major seconds, 1 minor third (E-G), 1 major third (C-E), 1 perfect fourth (G-C) and 0 tritones. 
    tntype -ia input > output

    Most prime forms of pitch class sets have a unique interval vector; however, some pairs of prime forms will generate the same interval vector. These prime form pairs are marked with Z when the -v option is given, with "Z" standing for "Z-related", "Z Correspondents" or "zygotic". Since two separate prime forms can have the same interval vector, the interval vector is an even more reduced form of the pitch-class sets than the prime form.

    Verbose Tn form description

    Extra properties of a Tn form can be included in the Tn type by using the -v option to give a verbose type. Meaning of extra markup:
    markup meaning
    S# Rotational symmetry of form. For example, (C, E, G♯) has the Tn form {0,4,8}, where "0" can represent either C, E, or G♯ since all three pitch-classes are separated by 4 semi-tones: {0,4,8}T0 = {0,4,8}T4 = {0,4,8}T8. Thus the -v option will add the mark "S4" since this form has a pitch-class rotational symmetry of 4 semi-tones. Other symmetric examples are fully diminished triads which are S3, wholetone scales which are S2, and the chromatic scale which is S1.
    * An asterisk mark after a Tn name indicates that the "A" and "B" forms (the prime form and its inversion) will generate the same pitch-class set. This means that the inversion of the prime-form will yield the prime-form for any type marked with "*". 3-11 has different Tn form when inverted, since (C, E♭, G) is 3-11A, while (C, E, G) is 3-11B, with the E/E♭ being different pitch classes which produce the same prime form when included in the set (C, G). The inversion of (C, F, G), however, is also (C, F, G), so it will have a "*" after the type: 3-9*, meaning that there are not A/B variants of the prime form.
    < Used to indicate that the complement of the prime form pitch-class set has the same inversional bifurcation.
    Z A "Z" mark indicates that there is another prime form which will generate the same interval vector description of the pitch-class set.
    .. Follows a "Z" marker indicating the paired prime form which has the same interval vector content. 
    tntype -va input > output

    Here is a list of all possible Tn prototypes for pitch-class sets which have rotational symmetry:

    Diatonic pitch-class sustain markings

    By default, the -d option will place parentheses around pitch classes which start at the beginning of the sonority, and only occur as sustained notes tied over from the previous sonority. The -S option will remove these parentheses. 
     tntype -da input > output

     tntype -Sad input > output

    Onset/Sustain markers

    The -x option can be used to mark Tn types by appending one of two characters: (1) 'x' if all pitch-classes are started at the beginning of the sonority (in other words, all pitch-classes are represented by at least one note onset); (2) 's' if any pitch-class is only represented by notes which are sustained from a previous sonority. If a pitch class is represents by both note onsets in the sonority region and sustained notes tied over from a previous sonority, then the note onset has priority in the x/s labeling decision. 

    tntype -xa input > output

EXAMPLES

    Count Tn sonorities in Bach chorales

    Here is an example of how to count all of the Tn types by sonority which are present in this collection of the J.S. Bach 4-part chorales: 
    tntype *.krn | rid -GLId | grep -v = | sort | uniq -c | sort -nr
    Meaning of each process in the command chain:
      tntype *.krn Do the T analysis on all files in the directory with filenames that end in ".krn", generating a Forte-number description of the Tn type.
      rid -GLId Remove Humdrum file structure from the analysis data (standard Humdrum Toolkit command).
      grep -v = Remove lines which contain an equal sign which represent barline data rather than analysis data (standard Unix command).
      sort Sort data into alphabetic order in preparation for input into uniq (standard Unix command). barline data rather than analysis data.
      uniq -c Remove adjacent duplicate lines, counting the number of successive lines in the input which are the same.
      sort -nr Sort the output from uniq in reverse numeric order, so that the most common Tm types are listed first.

    The most common Tn type in Bach chorales is 3-11B (major triad), with the minor triad occurring half as often (there are more chorales in a major key than a minor key, so this is somewhat to be expected). The most common sonority with a cardinality of 4 is 4-27B which is a dominant seventh chord (or German augmented sixth chord).

    To also print the Tn type's form and a brief musical description of the sonority's pitch class set, you can use a for loop in the bash shell (the for loop being necessary because Humdrum Extra programs cannot yet handle multiple segments of music in single data stream): 

     for i in *.krn
 do
    tntype -a $i | tntype -fa | tntype -Da | extractx -s '$2-$' | ridx -GLIMd
 done | sort | uniq -c | sort -nr > output

    In this case, the most common non-chordal sonority is {027}, such as (C, D, G), probably in the form of a 4-3 suspension, such as GCD → GBD.

    Identify the most common sonority transitions in Bach chorales

    tntype *.krn | grep -v = | context -n 2 | rid -GLId | sort | uniq -c | sort -nr
    Meaning of each process in the command chain:
      tntype *.krn Do the T analysis on all files in the directory with filenames that end in ".krn".
      grep -v = Remove lines which contain an equal sign which represent barline data rather than analysis data This is necessary so that context does not mix data and barlines, (standard Unix command).
      context -n 2 For each data element, include the following datum on the current line so that a context of 2 adjacent elements is stored on each data line. (Humdrum toolkit command).
      rid -GLId Remove Humdrum file structure from the analysis data (Humdrum toolkit command).
      sort Sort data into alphabetic order in preparation for input into uniq (standard Unix command). barline data rather than analysis data.
      uniq -c Remove adjacent duplicate lines, counting the number of successive lines in the input which are the same.
      sort -nr Sort the output from uniq in reverse numeric order, so that the most common Tm types are listed first.

      The most common transition is a major chord followed by a major chord. The second most common transition is a major chord followed by a dominant seventh chord:

      To get a more detailed (and interesting) analysis of the sonority transitions, add the -t option to preserve the relationship between the Tn type and the norman form. 

      tntype *.krn | grep -v = | context -n 2 | rid -GLId | sort | uniq -c | sort -nr

      In this case the most common transition is from a D major chord to a D dominant seventh chord (a V-V7 movement). The next most common transition is from a D major triad to a G major triad (a V-I movement). The third most common being D dominant seventh to G major (a V7-I movement).

      The above analysis is a bit too specific, while the one just before it is a bit too unspecific, so here is a third method which transposes each chorale to C major/minor (as the primary key) before examining the sonority transitions: 

       for i in *.krn
 do
    transpose -k c $i | tntype -t | grep -v = | context -n 2 | rid -GLId
 done | sort | uniq -c | sort -nr

      In this case the most common sonority transition is again between a V chord and a V7 chord. The second most common transition is between V7 and I, third: V and I, fourth: I and I, fifth: V to v, sixth: I to V. Keep in mind that these are sonority transitions and not chordal transitions, since there may be non-harmonic sonorities separating two adjacent chordal sonorities.

      3-9 Tn type

      As an interesting application of the tntype to functional harmony analysis, let's look at the most common non-triadic sonority in Bach chorales which is the 3-9 Tn type. This sonority type is most likely a 4-3 suspension. If so, then the following sonority will be a 3-11A/B type. 
       for i in *.krn
 do
    transpose -k c $i | tntype -t | grep -v = | context -n 2 | rid -GLId
 done | grep 3-9 | sort | uniq -c | sort -nr
      Looking at the extracted data, the most common application of the 3-9 sonority in Bach chorales (268 times without following repeats in the scores) is as a 4-3 suspension on the V chord. Occuring about 3.5 times less frequently (96 times), the 3-9 is used to create a 4-3 suspension on I. The next most common use is to create a suspension on VII (63 times), then on V/V (45 times). The most common non-suspension use of 3-9 is to transition into V, such as from (G, A, D) to (G, B, D) in C major, which occurs 43 times.

      Here is a plot of the functional position of the 3-9 sonority in Bach chorales (lumping major an minor keys together) when presuming that the 3-9 type functions as a 4-3 suspension (which is mostly but not always true):

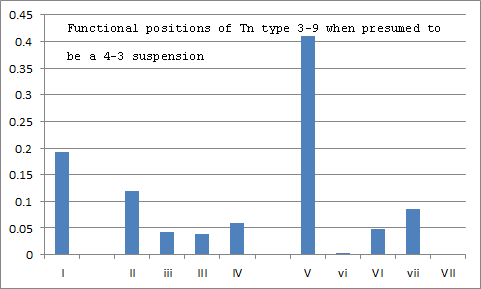
      Data extraction used to create the above histogram: 

       for i in *.krn
 do
    transpose -k c $i | tntype -t | ridx -GLIMd
 done | grep 3-9 | sort | uniq -c | sort -nr

      Onset versus sustain sonorities in Beethoven string quartets

      The -x option can be used to distinguish between sonorities which contain all pitch classes starting at the beginning of the sonority/Humdrum file line (Tn type marked with an "x") or cases where at least one pitch class is only sustained from a previous sonority (Tn type marked with an "x"). 
      tntype -x *.krn | rid -GLId | grep -v = | sort | uniq -c | sort -nr
      The results listed below demonstrate that major/minor chord sonorities (3-11 A/B) are more commonly approached through a sustained pitch class rather than having all pitch classes start at the same time.

    REFERENCES
      • Humdrum Toolkit program pcset.
      • Forte, Allen. The Structure of Atonal Music. New Haven: Yale, 1973.
      • Rahn, John. Basic Atonal Theory. New York: Longman, 1980.
      • Solomon, Larry. "The list of chords, their properties, and uses," Interface, Journal of New Music Research, Vol. 11 (1982).
      • Solomon, Larry. "Table of Pitch Class Sets," http://solomonsmusic.net/pcsets.htm.
      • Strauss, Joseph N. Post-Tonal Theory, Prentice-Hall, 1990.
      • Tomlin, Jay. "All About Set Theory." http://www.jaytomlin.com/music/settheory/help.html

    DOWNLOAD
      The compiled tntype program can be downloaded for the following platforms:
      • Linux (i386 processors) (dynamically linked) compiled on 26 Oct 2013.
      • Windows compiled on 29 Jun 2012.
      • Mac OS X/i386 compiled on 13 Nov 2013.

      The source code for the program was last modified on 26 Oct 2013. Click here to go to the full source-code download page.