keycor manpage

COMMAND

keycor -- Musical key identification by correlation.

keycor [options] [input] [> output]

Keycor is a generalization of the key-finding algorithm used in the Humdrum toolkit program key. While key is limited to a fixed set of key-weightings, keycor has a selection of 5 preset weightings, plus the ability for users of the program to provide their own set of weightings.

Pearson correlation is used by the program to identify the best key. Correlation takes two sequences and calculates a value between -1.0 and +1.0. An absolute correlation value near zero indicates a poor match, while a value of +1.0 indicates a good match. Using the Krumhansl-Schmuckler algorithm, Pearson correlation values are calculated between a histogram of the twelve-tone pitch-classes in a musical sample and each of the 24 major and minor key profiles.

Here is the mathematical definition of Pearson correlation: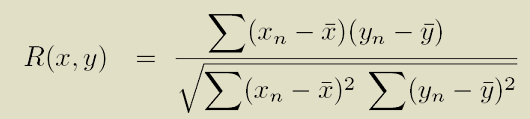

x is a histogram of pitch-classes extracted from a musical score. y is a list of the weighting values for each twelve-tone scale degree in a particular key. x-bar and y-bar are the average value for each input.

Generating a pitch histogram

An input pitch histogram for the Krumhansl-Schmuckler key-finding algorithm counts the duration of each pitch-class chroma present in the music. The -D option can be used to turn off duration weighting of note attacks (so that only note attacks and not note durations are stored in the input histogram). Here is an example segmenent of music:


Beneath the music is a list of the twelve pitch-classes present in the example, along with a count of how many eighth-notes worth of duration for each pitch class. Therefore the first input list to the correlation calculation is: (8, 0, 0, 0, 2, 11, 0, 5, 7, 0, 5, 2).

The second input into the correlation calculation is a list of weightings for the major/minor key being compared to. For example, using the simple weight set below the second input would be: (2, 0, 1, 0, 1, 1, 0, 2, 0, 1, 0, 1). And the resulting correlation value is 0.35.

The same process is continued, treating C-sharp/D-flat as the tonic note (which is equivalent to rotating the key-weights to the right by one element: (1, 2, 0, 1, 0, 1, 1, 0, 2, 0, 1, 0) (or equivalently, rotate the pitch-class histogram one element to the left). In this case the correlation value with C-sharp major and the extracted histogram is 0.25. Since 0.25 is less than 0.35, the algorithm thinks that the music fits C major better than C-sharp major. This process continues for the 10 other major keys, and also the 12 minor keys, and the key which generates the highest correlation value is presumed to be the actual key of the music:

C Major	0.35		C Minor	0.60
D-flat Major	0.25		C-sharp Minor	-0.38
D Major	-0.67		D Minor	0.03
E-flat Major	0.35		E-flat Minor	0.00
E Major	-0.48		E Minor	-0.29
F Major	0.64		F Minor	0.79
F-sharp Major	-0.16		F-sharp Minor	-0.60
G Major	-0.25		G Minor	0.12
A-flat Major	0.41		G-sharp Minor	-0.22
A Major	-0.54		A Minor	0.00
B-flat Major	0.48		B-flat Minor	0.54
B Major	-0.38		B Minor	-0.60

For the above musical example, the highest correlation corresponds to F minor, which generates a correlation of 0.79.

By default keycor uses the same weightings as key. These weightings are the experimentally-derived probe-tone ratings of Krumhansl and Kessler (listed below). The above table of calculations and search for the key which yeilds the maximum correlation value can be expressed mathematically in the following equation for the Krumhansl-Schmuckler key-finding algorithm: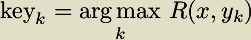

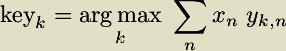
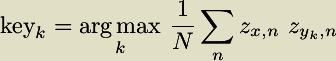
where x is the pitch-class histogram, y_k is a particular scale-degree weighting set for a particular key, and k is an index over all 24 major and minor keys being tested. The Krumhansl-Schmuckler key-finding algorithm is similar to an earlier algorithm developed in the 1960's by James Gabura which can be calculated instead if you specify the -G option: In this algorithm, the histograms and key weightings are not normalized before doing a dot product between the two input vectors. This will tend to cause problems in choosing between the best key in different modes (so it is more difficult to choose whether the best major or the best minor key is the overal-best answer). The similarity between the two algorithms can be seen by expressing the Krumhansl-Schmuckler algorithm in terms of z-scores: where N is the number of pitch-classes (12), z_p is the z-score version of the sequence p.

Key-profile weights

There are 5 preset key-profile weight sets available in the keycor program. By default, the Krumhansl-Kessler weights will be used. Other weights can be selected with the option listed above each set in the following table:

Krumhansl-Kessler probe-tone profiles (default): **kern **number C 6.35 C# 2.23 D 3.48 D# 2.33 E 4.38 F 4.09 F# 2.52 G 5.19 G# 2.39 A 3.66 A# 2.29 B 2.88 c 6.33 c# 2.68 d 3.52 d# 5.38 e 2.60 f 3.53 f# 2.54 g 4.75 g# 3.98 a 2.69 a# 3.34 b 3.17 *- *-

Aarden-Essen continuity profiles (--aarden): **kern **number C 17.7661 C# 0.145624 D 14.9265 D# 0.160186 E 19.8049 F 11.3587 F# 0.291248 G 22.062 G# 0.145624 A 8.15494 A# 0.232998 B 4.95122 c 18.2648 c# 0.737619 d 14.0499 d# 16.8599 e 0.702494 f 14.4362 f# 0.702494 g 18.6161 g# 4.56621 a 1.93186 a# 7.37619 b 1.75623 *- *-

Simple pitch profiles (-s): **kern **number C 2 C# 0 D 1 D# 0 E 1 F 1 F# 0 G 2 G# 0 A 1 A# 0 B 1 c 2 c# 0 d 1 d# 1 e 0 f 1 f# 0 g 2 g# 1 a 0 a# 0.5 b 0.5 *- *-

Bellman-Budge chord-based profiles (--bellman): **kern **number C 16.80 C# 0.86 D 12.95 D# 1.41 E 13.49 F 11.93 F# 1.25 G 20.28 G# 1.80 A 8.04 A# 0.62 B 10.57 c 18.16 c# 0.69 d 12.99 d# 13.34 e 1.07 f 11.15 f# 1.38 g 21.07 g# 7.49 a 1.53 a# 0.92 b 10.21 *- *-

Temperley-Kostka-Payne chord-based profiles (--temperley): **kern **number C 0.748 C# 0.060 D 0.488 D# 0.082 E 0.670 F 0.460 F# 0.096 G 0.715 G# 0.104 A 0.366 A# 0.057 B 0.400 c 0.712 c# 0.084 d 0.474 d# 0.618 e 0.049 f 0.460 f# 0.105 g 0.747 g# 0.404 a 0.067 a# 0.133 b 0.330 *- *-

Non-standard pitch profiles can be specified in a file which is given as input with the -w option. The weight file must have at least two spine: one **kern spine containing the pitch class -- upper case for major keys and lower case for minor keys; and a **number spine which contains the weighting for that pitch class and mode. There may be other spines in the file, but there should be only one **kern and **number spine in the file for predictable results. Here is an example pitchclass weight file using the same weights used with the -s option:

Here is a plot showing the relative weights of each scale-degree in the above five key-weighting sets. Major keys weights are shown in the top plot, and minor key weights in the bottom plot. The weights are normalized for direct comparison so that their standard deviation is 1 and the mean is 0 (which is what happens to the sequence when pearson correlation is used). KK (light blue) = Krumhansl-Kessler weights; S (red) = simple; KP (green) = Temperley-Kostka-Payne; BB (purple) = Bellman-Budge; AE (dark blue) = Aarden-Essen.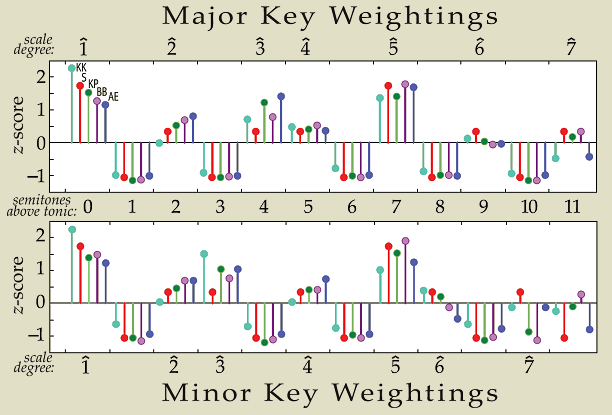



Weightings between the various sets are about the same for scale-degrees outside of the scale (particularly in the major scale). The Krumhansl-Kessler weights have the strongest weighting for the tonic in both major and minor keys. This causes these weightings to confuse the tonic and dominant more often than other weight sets. The sixth scale degree in major scales for all weight sets is mostly ignored.

General characteristics of preset key-weightings

Krumhansl-Kessler

Strong tendancy to identify the dominant key as the tonic.



Aarden-Essen

Weak tendancy to identify the subdominant key as the tonic.



Bellman-Budge

No particular tendancies for confusions with neighboring keys.



Temperley-Kostka-Payne

Strong tendancy to identify the relative major as the tonic in minor keys. Well-balanced for major keys.



Simple

Performs most consistently with large regions of music, becomes noiser with smaller regions of music.

Weight-set evaluations

The following table lists key-identification errors for five sets of key-profile weights. Each column represents a set of 24 compositions in all of the major and minor keys. 96 compositions from the Well-tempered Clavier, Books I & II by Johann Sebastian Bach, and 24 preludes, Op. 28 by Frédéric Chopin. Only errors are noted in the table, with blank cells indicating that the correct key was identified by the correlation algorithm using the specified key-profile weights.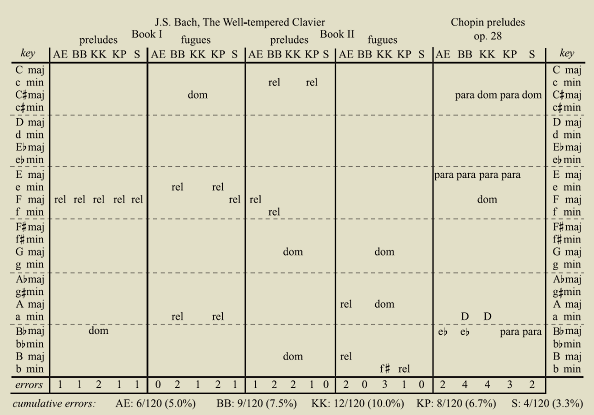



Errors are categorized as follows:

• rel is a modal error where the relative major or minor key is identified instead of the correct key. For example, if the correct key is A minor, and there is a rel label in the table, then that means that C major was identified by correlation rather than A minor.
• dom indicates that the dominant key was identified by the algorithm rather than the correct key.
• para -- the parallel key was identified rather than the correct key. For example C minor is the parallel minor key to C major and vice-versa.
Other more distant keys which are identified as the key rather than the correct key are labeled explicitly (5 cases).

Example usages of the keycor program are available on the keycor examples page.

Input arguments or piped data which are expected to be Humdrum files can also be web addresses. For example, if a program can process files like this:

       program file.krn

It can also read the data over the web:

       program http://www.some-computer.com/some-directory/file.krn

Piped data works in a somewhat similar manner:

       cat file.krn | program

is equivalent to a web file using ths form:

       echo http://www.some-computer.com/some-directory/file.krn | program

Besides the http:// protocol, there is another special resource indicator prefix called humdrum:// which downloads data from the kernscores website. For example, using the URI humdrum://brandenburg/bwv1046a.krn:

      program humdrum://brandenburg/bwv1046a.krn

will download the URL:

http://kern.humdrum.org/cgi-bin/ksdata?file=bwv1046a.krn&l=/brandenburg&format=kern
Which is found in the Musedata Bach Brandenburg Concerto collection.

This online-access of Humdrum data can also interface with the classical Humdrum Toolkit commands by using humcat to download the data from the kernscores website. For example, try the command pipeline:

      humcat humdrum://brandenburg/bwv1046a.krn | census -k

• Aarden, Bret. Dynamic Melodic Expectancy. Ph.D. dissertation. School of Music, Ohio State University; 2003.
• Bellman, Héctor. "About the determination of key of a musical excerpt" in Proceedings of Computer Music Modeling and Retrieval (CMMR): Pisa, Italy; 2005. pp. 187-203.
• Gabura, James A. "Music style analysis by computer" in Lincoln, Harry B., ed., The Computer and Music. Cornell University Press: Ithaca, New York; 1970.
• Krumhansl, Carol. Cognitive Foundations of Musical Pitch. Oxford Psychology Series No. 17. Oxford University Press: New York; 1990. pp. 37, 81-96.
• Sapp, Craig Stuart. "Key-Profile Comparisons in Key-Finding by Correlation." International Conference on Music Perception and Cognition (ICMPC 10); 2008, Sapporo, Japan.
• Temperley, David. Music and Probability. MIT Press: Cambridge, Mass.; 2007. p. 85.

key, mkeyscape, zscores.

The compiled keycor program can be downloaded for the following platforms:
• Linux (i386 processors) (dynamically linked) compiled on 28 Jun 2012.
• Windows compiled on 29 Jun 2012.
• Mac OS X/i386 compiled on 13 Nov 2013.
• Mac OS X/PowerPC (version 10.2 and higher) compiled on 13 May 2009.

The source code for the program was last modified on 21 Apr 2013. Click here to go to the full source-code download page.